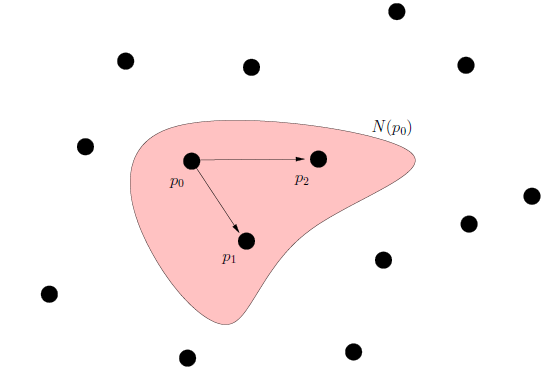
Proximity Catch Digraphs (PCDs) are special types of proximity graphs.
Definition:
-
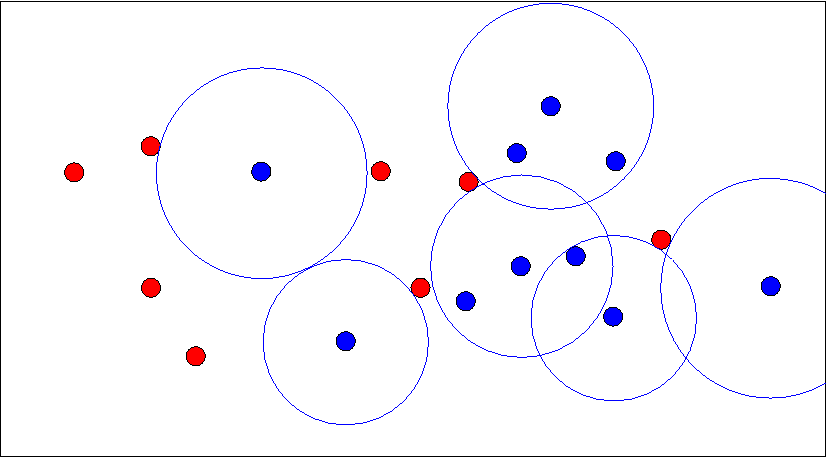
Let \( (\Omega,\mathcal{M}) \) be a measureable space. The proximity map \( N(.) \)
is given by \( N : \Omega \longrightarrow \wp(\Omega) \), where \( \wp(.) \) is the power
set functional. Hence, proximity region of \( x \in \Omega \) is denoted by \( N(x) \).
-
A point \( p \in N(x) \) is thought of as being "closer" to \( x \in \Omega \) than the points
in \( \Omega \setminus N(x) \).
-
The proximity catch digraph \( D=D(\mathcal{V},\mathcal{A}) \) has a vertex set
\( \mathcal{V}=\{y_1,\cdots,y_n\} \) and the arc set \( \mathcal{A}\) is defined by
\( (v_i,v_j) \in \mathcal{A} \) if and only if \(v_j \in N(v_i) \) for \( i \neq j \).
A. Manukyan & E. Ceyhan
Last modified: Oct 16, 2022

 |
 |
 |
 |